Sing

idea by Rainbow_sjy, solution by zhoukangyang, Rainbow_sjy

考虑如下性质：将 $(i,p_i)$ 画在坐标轴上，如果一个点向左上方（$i$ 变小，$p_i$ 变大）的方向移动，则限制一定更紧。

据此，我们可以只考虑所有 $p_i$ 为前缀最大值和前缀次大值的限制。

考虑枚举 $p_1$ 填什么。

如果 $p_1\le k+1$，直接对后面毫无限制。

如果 $p_1 > k+1$，则要求 $p_2,p_3,\dots,p_{p_1-k-1}$ 都 $\le k+1$。只有 $p_1$ 是前缀最大值，后面这段数也对更后面毫无限制。于是可以递归到继续填 $p$ 的一个后缀。

分析清楚排列的结构后，就可以计数了：

对于 整个过程中，一个前缀中只能有一个 $p_i > k+i$ 的；如果钦定了 $p_i > k+i$，那么后面的一段的转移系数是固定的。大概长成这样：

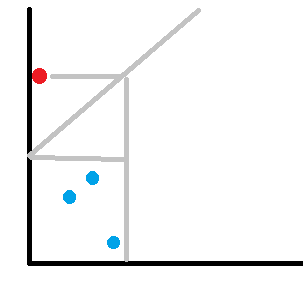
直接暴力 dp 是 $O(n^2)$，观察到长度相等的转移系数相等，可以多项式求逆做到 $O(n\log n)$。

对于排列有限制位置的情况，和上述 $O(n^2)$ 做法一样，注意一些细节。

希望市

idea by bulijiojiodibulido, solution by bulijiojiodibulido, zhoukangyang, chenxinyang2006

人类勇气之赞歌

idea, std, data by GeZhiyuan, solution by GeZhiyuan, zhoukangyang

首先不难有一个动态规划，用 $f_i$ 表示 $[1, i]$ 的答案。直接做就是 $O(n^2k)$ 的。

接下来用一些手段去优化转移，考虑从 $1$ 到 $n$ 扫 $r$，同步维护 $s_{u, l}$ 表示 $[l, r]$ 区间的第 $u$ 大。

考虑某一时刻如果有 $s_{u, l} = s_{u, l+1}$，那么后续过程中两者保持相等。考虑扫描过程中，如果出现了 $s_{u, l} = s_{u, l+1}$，就将两个直接合并成一段。然后暴力修改有更改的 $s_{u,l}$（对于合并过的连续段快速跳掉）。

可以证明这样暴力修改只会进行 $O(nk^2)$ 次：

• 考虑将 $a_r$ 加入时，对于某个 $l$，若存在 $s_{u, l} = a_r$ 则 $p_l = u$，否则 $p_l = k+1$。

• 且如果 $s_{u, l} = s_{u, l-1}$，则 $\forall v \in [1, u]$，都有 $s_{v, l} = s_{v, l+1}$。记 $h_l$ 表示最大的满足 $s_{u, l} = s_{u, l+1}$ 的 $u$，不难发现 $h_l$ 在扫描过程中不会减小。

• 不难发现有 $p_{l+1} \leq p_l \leq p_{l+1}+1$，因此 $a_r$ 对 $s_{u, l}$ 直接的修改只有 $k$ 段。
• 但考虑有些 $s_{u, l}$ 是继承了 $s_{u-1, l}$ 的值，由于我们快速跳过了值域相同的连续段，因此实际上只要考虑 $s_{u, l} \neq s_{u, l+1}$ 的位置即可：
  • 如果 $p_l \neq p_{l+1}$，这样的位置只有 $k-1$ 个，每个位置只要维护 $k$ 个信息，因此单次修改这样的位置修改不超 $k^2$ 个。
  • 如果 $p_l = p_{l+1}$，不难发现此时 $h_l$ 会增加 $1$，因此均摊总共只会对 $nk$ 个这样的位置进行修改，每个位置要维护 $k$ 个信息，因此总共也不会超出 $nk^2$ 次。

同理用 $t_{u, l}$ 表示 $[l, r]$ 的第 $u$ 小。至此我们知道了有效的区间修改只有 $O(nk^2)$ 次，接下来我们要尝试做到 $O(1)$ 的修改，这部分大家可能都知道该怎么做但比较 $\text{dirty work}$，需要选手有很大的勇气。

考虑将 $s_{u}$ 和 $t_{k-u}$ 这两个数组一起维护对答案的贡献；考虑进一步分析性质发现每一次修改都是一个后缀，用如下手段维护：

• 我们考虑用某种手段将下标划分成若干连续段，每段内用凸包单独维护，每段的凸包根据情况分为如下三种，假设其对应下标是 $[l, r]$：
  • 如果 $s_{u, l} = s_{u, l+1} = \dots = s_{u, r}$，则考虑称其为 A类，此时我们考虑对 $t$ 用凸包进行维护，对于每个 $t_{u, i} \neq t_{u, i+1}$ 的点，向凸包内插入 $(x - t_{u, i})^2 + f_{i-1}$，进一步发现实际上比较两个值的时候，$x^2$ 上的系数是相同的，因此实际上等价于插入直线。
  • 如果 $t_{k-u, l} = t_{l-u, l+1}=\dots=t_{l-u, r}$，则考虑称其为 B类，此时同理对 $s$ 用凸包进行维护。
  • 如果同时有 $s_{u, l} = s_{u, l+1} = \dots = s_{u, r}$ 和 $t_{k-u, l} = t_{l-u, l+1}=\dots=t_{l-u, r}$，那么称之为 C 类。这种直接可以快速修改和统计答案。
• 根据 “某一时刻如果有 $s_{u, l} = s_{u, l+1}$，那么后续过程中两者保持相等”，如果对 A类 直接进行修改，其只可能要么继续保持 A类，要么变成 C类，对于 B类 和 C类 是类似的的，如果两个下标形成了一段，那么他们永远都可以在同一段。
• 考虑我们再尝试将连续段进行合并，如果有两个相邻的连续段可以合并成 A, B, C 类其中之一，那么我就强制让他们合并到一起。
• 这样可以证明，一个区间修改只会最多影响三个连续段。于是乎每次修改设计的连通块数是等规模的。
• 然后由于修改又是后缀，因此我们可以把后缀的连续段取出来，将修改作用于上面后依次尝试和前面合并即可。
• 由于 $r$ 增大时，许多东西的变化都是单调变优的，因此我们考虑如下维护过程：
  • 如果我们要修改某一个连续段，我们假设这个连续段是 A类 的，对于 B类 是对称的，而 C类 修改是容易的：
    • 如果我们是对 $s_u$ 进行修改，那么由于我们维护好了 $t$ 的凸包，且 $s_{u, l}$ 的变化一定也是单调的，因此只需要维护一个指针在凸包上暴力移动均摊就是对的。
    • 否则考虑必定是 $t_{k-u}$ 在这个区间上的一个后缀被修改，我们将这些直线直接插入凸包中不好插入，因为斜率不一定单调，可能被包含在当前凸包的斜率中，但根据 $t$ 的单调性和修改的单调性，你发现可以将其中一侧的直线直接全部从凸包中删除，因为这些线段是原本被修改的位置贡献的，新的一定更优。至此我们将那一侧的直线全部删除后正常维护凸包即可，均摊也是对的。
  • 而合并两个连续段呢？首先 C类 间的合并好做，如果 A类 和 C类 合并则可以认为先将 C类 转为 A类，而 A类 和 B类 没法合并。因此我们只需要想清楚 A类 和 A类 怎么合并即可，B类 和 B类 的合并是同理的：
    • 考虑到 $t_{k, u}$ 是单调的，因此我们合并两个连续段时，凸包的斜率不交（实际上至多有一个相同，但可以将较劣的直接弹掉），因此直接凸包合并即可。但发现这里需要支持 $O(1)$ 把两个序列拼起来，因此实际上凸包需要用链表维护顺序。
• 考虑维护对答案的贡献异常好算，答案是单调的，因此只需要每次发生修改时，把新的结果直接贡献到答案即可。

可能说的不是很清楚，因为确实细节太多！但至此我们实现了修改均摊 $O(1)$，时间复杂度 $O(nk^2)$，空间复杂度 $O(nk)$。