星图
idea, solution, std, data by Rainbow_sjy
这题本来定位是本场比赛的签到题,但似乎难到大家了。
打表可以发现符合条件的 01 串个数是 $2^k$ 个,有些位置是自由位,其他是固定位,于是我们来构造证明一下。
显然,只有 $i$ 为偶数的情况可能为“自由位”。且 $s_2 = 0$ 不是“自由位”。
首先要保证 $s_n$ 符合要求,这个相当于判树的重心是否有两个。
考虑倒着删点,一开始的重心是定的。我们想考虑如何得到第一个“自由位”。
- 如果重心 $\text{deg}\ge 3$:
一开始删的若干步,偶数位置必须 $s_i = 1$。
考虑最大的子树,我们试图删外面的点数,使得最大的子树中的点数和外面一样,这样可以成功做到第一个 $s_i = 0$。
在之后,只要保证重心有至少 $3$ 个子树有点没有被删,就可以任意控制偶数位的 $s_i$。
具体的,我们可以这样构造:控制重心最后一个删,对于剩下奇数个点时,重心的最大子树中的点数 = 重心的其他子树中的点数。然后下一步考虑先删 最大子树 还是先删 其他子树,就可以控制 $s_i = 0/1$。
- 如果重心 $\text{deg} = 2$:
一开始删的若干步,偶数位置必须 $s_i = 0$。
我们找到重心所在的极长链(dfs 到两端端点都 $\text{deg}\ne 2$),考虑树的带权重心,只有在删了若干个点后,带权重心会移到这条链的一个端点。
可以在这条极长链上任意删点,直到带权重心移到这条链的一个端点。在这个过程中,偶数位置必须 $s_i = 0$。
接下来我们把重心改成当前的带权重心,就变成了 $\text{deg}\ge 3$,且重心的最大子树中的点数 = 重心的其他子树中的点数的情况。可以套用上述的构造,使得之后每一位都为“自由位”。
p.s: 有人问我 checker 是怎么写的。有个好写的 $\log^2$ 做法,要砍的那条边肯定是 dfs 序一段 $\frac{m}{2}$ 长度的 lca,那 check dfs 序 rank $\frac{m}{2}$ 和 $\frac{m}{2}+1$ 这两个点的祖先即可,可以倍增. 如果要做到单 $\log$,可以维护带权重心在哪里,但是比较难写。
欢迎来到最前线
idea, solution, std, data by myee
嗯其实我不太清楚为啥正赛时会有一些奇怪的挂分……总之祝大家 NOI 好运吧。
其实本题可以不绑包全多测塞一个点的,但是因为换成多测只是增加代码难度而不改变分数,没啥意义所以否决了。
我们分做法来介绍吧。
爆搜、状压等指数级做法
估计最多能拿 $\rm14pts$ 吧。
其实我不太确定 $n\le20$ 有没有啥独特的做法。
动态规划
为了方便考虑,我们对所有物件进行排序,把跳蚤设做红点,冰球设做蓝点,那么我们就是要选取若干对红蓝匹配,使得距离总和尽可能小。
考虑 DP,设 $f(n,a,b,k)$ 表示 $[1,n]$ 区间内选择了 $a$ 个向右出去匹配的红点,$b$ 个向右出去匹配的蓝点,区间内已经匹配了 $k$ 次,此时的最小代价。(向外匹配的部分贡献提前计算)
每次在右端加入一个点,可以选择是按照哪种方式进行匹配,或者不参与匹配。
复杂度看起来是 $O(n^4)$ 的?
注意到 $a,b$ 如果都不是 $0$,就意味着有红蓝同时向右匹配,这显然是不合理的:内部自我消化掉显然不劣。
于是 $a,b$ 中至少有一个是 $0$,状态数大量减小。
复杂度 $O(n^3)$。
大概是不超过 $\rm38pts$。
费用流
这题题意都明摆着二分图匹配了,那肯定可以想到网络流!
这个“最小费用 $k$ 次匹配”,那是不是直接跑个费用流就行了?
点数 $n$,边数 $O(n^2)$,跑 $n$ 轮,每轮一步增广。
复杂度看起来是 $O(n^4)$?写个原始对偶应该就是 $O(n^3)$ 左右了。
大概和 DP 做法得分一个水平,实际由于常数说不定更快一点。
通过合并重点,可能可以通过 $v\le200$?
不过费用流模型提醒了我们一件事情:答案是凸的。
(所以如果答案的值域很小可能只有根号答案值域段等差数列……不过这个性质没有啥用)
模拟费用流
考虑我们费用流的增广路在这里是什么情况:设跳蚤是 $R$,冰球是 $B$,那么增广路总是长成 $R\sim B-R\sim B-R\sim\cdots\sim B-R\sim B$,其中 $B-R$ 表示之前的匹配,$R\sim B$ 表示新的匹配。
我们知道,不可能出现形如 ${\color{green}R}{\color{orange}B}{\color{orange}R}{\color{green}B}$ 的结构,满足外侧的 $\color{green}R,\color{green}B$ 匹配,内侧的 ${\color{orange}R},{\color{orange}B}$ 匹配:不然我们调整不劣。
因此容易发现我们这样的增广路总是满足坐标逐渐增加,或者坐标逐渐减小。
以坐标逐渐增加为例,我们让每个 $R$ 找到右侧最近的满足“当前不是向左匹配的最优 $B$”,从右往左扫描一轮就可以计算出所有可能优的增广路并统计出增广的贡献,从而 $O(n)$ 找到增广路。
复杂度应该是 $O(n^2)$ 左右,拿到 $\rm50pts$。
通过合并重点,可能可以通过 $v\le200$?
到这里后就有不少同学开始各显神通了,比如用数据结构维护这个结构。使用线段树维护然后找到变化位置暴力改的复杂度是错的(感谢 chenxinyang2006 的验题代码发现了这个,于是数据对着卡了),使用分块维护是正确的不过常数巨大无比,大概能过 $50000$ 吧。
这样就能拿到不超过 $\rm76pts$。
反悔贪心
观察到如下重要性质:如果两个点之间发生了匹配,这两个点间的点一定都已经被匹配了,并且是同向的匹配。
为什么?打个比方,假设当前的匹配形如 ${\color{green}R}R{\color{green}B}$,其中外侧的 ${\color{green}R}{\color{green}B}$ 发生了匹配,而中间的点没有匹配,那么我们调整肯定不劣。至于同向匹配,我们在上个做法里已经证明过了。
这个性质意味着,匹配是一段段的,每段内的贡献可以用前缀和状物直接 $O(n)$ 预处理 $O(1)$ 查询。并且我们在进行增广路的时候,只用考虑向已经完全匹配的区间左右一个点增广。
那么我们考虑这个反悔贪心算法:用 set 或者并查集维护当前还没被匹配的点,用堆维护当前的可选增广路左右端点列表。每次选出一个最优的合法增广,进行匹配并加上贡献的变化值。然后尝试向左右外侧各种找到一个还没被匹配的点,如果能作为增广路的端点就塞进堆中。
这样复杂度就是 $O(n\log n)$ 的了,可以轻松通过本题。
闵可夫斯基和
能不能进一步仔细观察一下这道题目的性质?
注意到匹配既然总是分区间的,我们设跳蚤是 $1$,冰球是 $-1$,做前缀和。那么只有前缀和相同的两点之间的区间,才可以构成一段合法的匹配。
并且,只有相邻的前缀和相同点,才有可能使得左端和右端构成匹配。
这也意味着,对于一个点来说,其最多只可能和左侧某个点以及右侧某个点构成匹配。
因此这样的情况下,可能的匹配构成了若干条链,每条链形如 $RBRBRB...RB$。
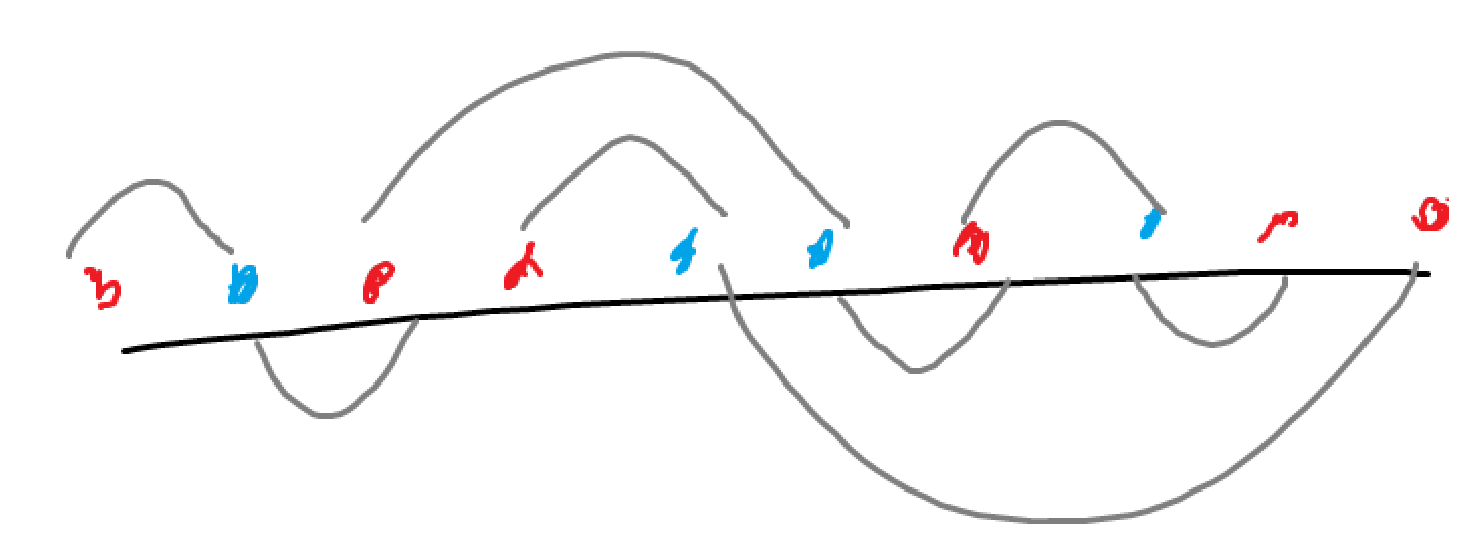
那么我们可以计算出每条链内部对每种 $k$ 的最优匹配,最后再对每条链的答案做闵可夫斯基和即可。我们已经用费用流证明了这个函数是凸的了。
而单条链可以通过维护前缀答案的凸壳来实现,也可以通过分治合并来实现。
滑冰
idea, solution, std, data by shr
算法零
观察到本题难以构造出足够强的数据,选手可以实现各种搜索或乱搞。
期望得分 $?$ 分。
算法一
对于每一个格子,向其走一步后会停留的点连边。得到一个有向图,缩强连通分量。
对于每个格子,上下为同一 SCC,左右为同一 SCC。一个格子被经过当且仅当这两个 SCC 至少有一个被经过。
要在缩出来的 DAG 上找到一条从起点开始的路径。可以转化为选一个点集两两可达,起点可达所有点,且满足上面提到的两个至少选一个的限制。
可以使用 2-SAT 解决。时间复杂度 $O(n^3)$,使用 bitset 优化可以做到 $O(\frac{n^3}{w})$。
期望得分 $40\sim52$ 分,实际得分 $40\sim 68$ 分。
算法二
分析每一个 SCC 的性质,存在以下几类 SCC:
- 如果不选不能经过所有属于该 SCC 的格子:根据连边方式,发现这个 SCC 需要存在一个不向外连边的点。
- 入度为 $0$,点数为 $1$ 的 SCC,对应到原图是一个四周都没有障碍的格子,会对两个 SCC 产生至少选一个的限制。为了方便后面的讨论,先将这种 SCC 从缩点后的图中删除,最后单独处理。
剩余的 SCC,可能会由前面的限制间接导致必须选。对于所有 SCC,需要保证若其未被选,所有其直接连边的 SCC 都必选。实际上就是每条边两个端点至少选一个。
路径的终点一定是唯一的出度为 $0$ 的 SCC。现在考虑倒着构造出路径。首先有一个结论:一定存在合法解是最长路径。假设存在一条不是最长链的合法路径,那么最长链上任意两个相邻被选的点之间距离至多相差 $2$,否则不能满足每条边两个端点至少选一个的限制。最长路径上相邻被选的点在合法路径上距离也不超过 $2$,如果距离等于 $2$,可以直接替换;否则将最长路径中夹在中间的点加入仍然合法。
记点 $u$ 到终点的最长路径为 $d_u$,可以按 $d_u$ 分层,每一层至多选一个点。接下来暂时只考虑最长路 DAG 上的边。如果有唯一的后继 $v$ 满足 $d_v=d_u-1$,则 $v$ 是必选的。考虑若没有经过 $u$,为了满足边的限制 $v$ 必须经过;否则 $u$ 一定下一步走最长路,也要经过 $v$。对应后继不唯一的情况,首先可以确定 $u$ 是必选的,因为其后继不能同时经过。同时大部分后继的后继都是必选的,考虑直接确定出 $d_w=d_u-2$ 这一层的 $w$,可以发现 $w$ 就是所有 $v$ 的后继集合的交,且这个交集大小需要恰好为 $1$。之后只要让 $d_v$ 这一层有一个限制是若干个 $v$ 里至少选一个即可,注意由于每层至多选一个点,所有需要对每层维护一个点集,表示最后的候选点,没有遇到这个限制就求交。这个限制可以用前缀后缀优化 2-SAT 建边解决。
令 $\max d_u=mx$,根据上面的讨论,可以发现相邻两层至少有一个必选点,那么 $mx$ 这层或 $mx-1$ 这层一定有必选点了。如果 $mx$ 这层有必选点,可以直接跑一次 2-SAT 判断是否有合法路径;否则需要判断 $mx-1$ 这层的必选点和若干 $mx$ 这层的点能否作为起点。
时间复杂度 $O(n^2)$ 或 $O(\frac{n^2}{w})$,期望得分 $76\sim88$ 分。
算法三
判断 $mx-1$ 这层的点是否可以作为起点,如果可以,所有 $mx$ 这层的点也可以作为起点。否则若 $mx$ 这层内部存在两个点至少选一个的限制,那么该层最多只有两个合法的起点。
经过一些对拍和尝试发现构造不出其它可能让 $mx$ 这层有至少两个合法起点的情况。出题人太菜不会证明,这题还有很多没用上的性质和难以证明或证伪的结论,读者可以尝试加强本题。
时间复杂度 $O(n)$ 或 $O(n\log n)$,期望得分 $100$ 分。
算法四
zhoukangyang 指出不用算法三的结论也可以线性:
优化判断 $mx$ 这层哪些作为起点的过程。令 $u_0$ 为 2-SAT 中代表不选 $u$ 的点, $u_1$ 表示选 $u$ 的点。判断选 $u$ 是否合法,需要连一条 $u_0\to u_1$ 的边,然后判断是否合法。可以发现,不合法当且仅当之后 $u_0$ 和 $u_1$ 被缩点了,那么需要判断 $u_1$ 能否到达 $u_0$。发现 $u_1$ 的出边只有所有 $u'_0$,其中 $u'$ 是 $mx$ 这层所有不等于 $u$ 的点。于是问题转化为判断一个 $u_0$ 能不能被其它 $u'_0$ 所到达。这只需要在缩点后的 DAG 上做一个 DP,记录每个点能否被某个 $u_0$ 到达即可。
下面写的部分分做法 credit from Rainbow_sjy, Kubic
$O(n^3) , O(n^3/w)$ 做法
把矩阵划分成横竖的极长段。
每个条建一个 01 变量表示到不到。
每个点必须在两个条中至少经过一个,是两个条之间的一个限制。
判断一个条是否能成为起点:这个条不能到的条必须为 false。
对于一条路径,上面没有两个点是互不可达的,所以如果两个点互不可达,连边 A true->B false。
跑 $n$ 次 2-SAT 为 $n^3$。
可以 bitset 存边,用 kosaraju 替代 tarjan,一次 2-SAT 为 $n^2/w$,可以做到 $O(n^3/w)$。
期望得分 52。
$O(n^2) , O(n^2/w)$ 做法
还是把矩阵划分成横竖的极长段。
然后如果一个线段可以在端点处转到另一个,那么就连有向边。
一条路径合法的一个必要不充分条件是,有向图上每条边的两个端点中至少经过一个。
而每个点仅有两条出边,考虑进行一些分析。
假设当前点是 $u$,出边连到 $v,w$ 如果 $v$ 不能到达 $w$,那么 $u$ 必须在路径上,否则 $u\to w$ 这条边可以删掉。
所以现在就是,出度为 $2$ 的点全部必选,剩下的点出度为 $0$ 或 $1$,要找一条路径。
最后结构长这样

每个 两条路径 都只能选一个,且对于每个点,需要 它的横条和竖条 至少有一个经过。
如果有一边链长 $\ge 2$,就必选了,只有链长为 $1$ 的才是可选。所以最上面是一个菊花。
只有最上面菊花上的点有可能为答案,可以 2-SAT,限制一堆变量中只有一个是 1。
由于前面删边要判点可达性,复杂度 $O(n^2/w)$。
期望得分 88。
$O(n)$ 做法
上述做法的两个 $O(n^2/w)$ 部分可以优化。具体见上方的官方题解。

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号