决战库尔斯克

idea, solution, std by Graygoo_401, solution' by return20071007, zhoukangyang, data by Graygoo_401, Rainbow_sjy.

考虑把序列最大值 $mx$ 求出来，按照是否严格大于 $mx \over 2$ 分成两部分，分别称为 $A$ 和 $B$。$A$ 内部的答案显然为其极差，$B$ 内部的答案可以递归下去求，考虑怎么求出两部分之间的贡献。

设 $A$ 的极差为 $d$，对于一个 $v \in B$，如果有 $v \leq d+1$，则它不会更新答案；否则容易发现 $A$ 中元素对 $v$ 做除法后最多得到两种商，枚举商统计贡献即可。

这样子得到 $O(n \log n \log V)$ 解法，由于常数很小足够通过。

以上做法存在更简洁形式：排序后直接倒着扫，如果当前数已经小于答案则退出，否则每次暴力向后枚举所有可能的商。容易发现这个东西和上面做法等价。

以下介绍一个来自 UT 老师的确定性 1log 做法。

假设现在反扫到 $A$，遇到了 $x=XA+A-U$ 和 $y=(X+1)A+V$ 需要二分其分界点，其中 $0\lt U\le A$，$0\le V\lt A$。根据经典结论有 $y-x\lt A$。

取 $y\lt z\le\frac{xy}{y-x}(1-\frac Ax)=\frac{y(x-A)}{y-x}$，则 $\frac zx-\frac zy=1-\frac 1X\lt1$，于是 $\lfloor\frac zx\rfloor=\lfloor\frac zy\rfloor$ 或 $\lfloor\frac zx\rfloor=\lfloor\frac zy\rfloor+1$。

如果 $\lfloor\frac zx\rfloor=\lfloor\frac zy\rfloor+1$，设 $z=xa+p=y(a-1)+q$，其中 $a=\lfloor\frac zx\rfloor$，则 $z\bmod y=q$。注意到此时 $x\le x+p=(y-x)(a-1)+q\le(y-x)\times\frac zy+q=x(1-\frac Ax)+q$，于是 $q\ge A$。但我们的 $A$ 被反扫到而非直接剪枝，矛盾！

所以不可能出现这种情况。于是区间内的所有 $z$ 都满足 $\lfloor\frac zx\rfloor=\lfloor\frac zy\rfloor$。设 $z=xa+p=ya+q$，其中 $a=\lfloor\frac zx\rfloor$，那么 $z\bmod x=p=(y-x)a+q$。由于 $A$ 没有被剪枝，可知 $p\lt A$，也即 $(U+V)a+q\lt A$。于是 $0\le Va+q\lt A-Ua\le A-U=x\bmod A$。同时注意到 $z=ya+q=Va+q+(X+1)Aa$，于是 $z\bmod A=Va+q\le x\bmod A$，我们可以直接跳过这部分 $z$。

总而言之，我们接下来可以一直无视直到 $z\ge\frac{xy}{y-x}(1-\frac Ax)\gt(X^2-1)A$。那么对于一个固定的 $A$ 和值域 $W$，只需要二分 $O(\log\log V)$ 次。

如果直接进行二分，复杂度为 $O(n \log n \log \log V)$。

但是众所周知地，整数后继存在 $\log \log V$ 求法。不过如果需要严格确定性，这里就不能上传统 y-fast trie 的哈希表，我们需要字典树上预处理一个点按照某种轨迹连走 loglog 步的结果，这样在字典树上定位的复杂度即降到 $O({\log \over \log \log}+\log \log)$，后面同正常即可。

除 UT 做法以外，我们还有一个来自于 zak 的非确定性 1log 以及一些不会证也不会卡的做法（二进制分组，但是先去重并且能不二分（只有一个商）就不二分，详见 std 代码），如果有大神会证或卡了可以教教我。

决战尘雨巷

idea by Coffee_zzz, solution by return20071007, std,data by Milmon.

算法零

对于子任务 1，只需要一开始做反转，然后不断向同一个方向走，直到遇到 $1$ 为止，此时走的步数即为 $n$。

算法一

考虑倍增，假设当前已经确定 $n > 2^{k - 1}$，现在需要处理 $2^{k - 1} < n \leq 2^k$ 的情况。比较简单的做法是，不断朝一个方向走 $2^k$，记录这些位置的值，然后反转下一个位置，再走回来并查询新值，如果发现与原先的值不一样，那么反转位置与该位置的差即为 $n$。花费的代价是 $\mathcal{O}(n)$ 的，但是常数较大。

添加如下优化：

• 注意到一轮结束后，总是已知一个区间并且当前位于区间的一个端点处，于是只需要朝另一个方向继续走并记录值即可；
• 最后查询新值时，由于已经确定 $n > 2^{k - 1}$，所以前 $2^{k - 1}$ 个位置不需要查询。

这样一轮花费的代价为 $2.5 \times 2^k$，所以比值最大时约为 $8$（需要注意找到 $n$ 之后剩下的部分不需要继续走，并且比值在 $n = 2^k + 1$ 时取到极值）。

然而事实上以 $2$ 为基数倍增并不是最优的，具体地，有两种可行的优化方法：

• 设倍增基数为 $k$，则比值为 $\frac{k (4k - 3)}{k - 1} - 2(k - 1) = \frac{2k^2 + k - 2}{k - 1}$，在 $k = 1 + \frac{1}{2} \sqrt{2}$ 时取到最大值 $5 + 2 \sqrt{2}$；
• 可以直接 DP 出每次倍增最优的分界点，在 $n \leq 2 \times 10^3$ 的限制下最优比值约为 $7.5$。

这两种方法都可以通过子任务 2。

算法二

设初始位置为第 $0$ 个位置，向后移动的过程中，维护“第 $0$ 个位置为 $1$，其余位置均为 $0$”的状态以及一个候选答案。具体地：

• 若当前走到第 $i$ 个位置并且值为 $1$，那么反转当前位置，并且标记 $i$ 为一个可能的答案；若 $i$ 是答案，那么必须满足接下来 $i$ 个位置均为 $0$，我们将在 $2i$ 处检验这个答案，而之前的候选答案未被检验，可以舍弃。
• 如果值为 $0$ 什么都不用做。除非现在到达了候选的答案 $x$ 的两倍处，此时需要反转当前位置并往回走 $x$ 步，检验位置 $x$ 是否变为 $1$。如果是则确认答案为 $x$，否则答案被舍弃，走回 $2x$ 并把 $2x$ 反转为 $0$ 即可。

这样会在走到 $2n$ 时得出答案，走的过程加上查询位置共 $4n$，检验答案时所有 $[x + 1, 2x]$ 形成若干个不相交的区间，长度总和不超过 $2n$，代价共 $4n$。而最后得出答案之后不需要走回去，可以节省 $n$ 的代价，故比值最大为 $7$，大约可以得到 $65$ 分。

算法三

调整算法二。假设当前已经维护第 $p$ 个位置为 $1$，而 $0 \sim p - 1$ 均为 $0$，并且已知答案 $> p$。每次找到下标 $> 2p$ 的第一个 $1$ 所在的位置 $p'$，若答案 $\leq p'$，则答案一定正好是 $p' - p$。反转并往回走到 $p$ 处检查即可，返回 $p'$ 时将中间这一端全部置为 $0$ 即可。

这部分总代价为 $4(p' - p)$。而得出答案后不需要走回去并且清空，所以总代价为 $6n + \mathcal{O}(\log n)$，大约可以得到 $86$ 分。

算法四

基于算法一优化。在算法一基础上，倍增过程中记一个 $B$，并且设倍增到 $2^k$，改为维护 $\frac{2^k}{B}$ 个位置的值，维护的相邻两个位置距离为 $B$，这样一个长度为 $2^k$ 的部分每 $B$ 个就有一个位置被记录。

修改时先走到序列的左侧一端，令这一端外连续 $B$ 个位置反转，再向右走遍历序列，在记录值的位置处检验值是否被修改，若被修改，那么就可以得到一个 $n$ 的大小为 $B$ 的范围。在此基础上为了快速确定 $n$ 的值，还需要将反转的 $B$ 个位置的右侧 $B$ 个位置修改为 $1, 0, \cdots, 0$ 作为标识，这样找到一个记录的值被反转时，只需要查询接下来 $2B - 1$ 个值，其中的标识一定是唯一的。

算法一中提到的优化仍然可以保留。那么已知 $n > 2^{k - 1}$，检验 $[2^{k - 1} + 1, 2^k]$ 区间内是否有答案的过程需要 $1.5 \times 2^k + \mathcal{O}(B + \frac{2^k}{B})$ 的代价。

$B$ 的值需要随着倍增过程动态调整，但是需要注意 $B$ 只能整倍数增加，否则会存在新的位置需要记录。总代价为 $5n + \mathcal{O}(B + \frac{n}{B})$（注意找到 $n$ 之后后面会省去一部分代价）。维护 $B = \mathcal{O}(2^{0.5k})$ 时代价即为 $5n + \mathcal{O}(\sqrt{n})$。

但是 $\mathcal{O}(\sqrt{n})$ 部分常数比较大 ，所以在子任务 3 中对 $n$ 较小时放宽了比值要求。

另外一种思路是维护一个每隔 $B$ 个就固定有一个 $0$ 的序列，走到序列一端后向外连续 $B$ 个位置均修改为 $1$，这样往回走的时候也能找出 $n$ 的范围；然后额外在 $1$ 后面加一个 $0$ 用来定位准确的 $n$。代价大约是 $6n$，调整倍增分界点可以更优一些。

决战中途岛

idea, solution, std, data by pp_orange

题解一

我们称 $y\ge |x|$ 的区域为可行区域。

我们“桶翻”和“机动”两步看做为同一时刻发生的一步，来刻画交替操作。我们注意到出发时距离原点的曼哈顿距离是奇数，所以"桶翻"的时候一定不会翻出可行区域的，我们把两步合并成一步后再把坐标轴旋转 $45$ 度，这样如果我们现在位于 $(p,q)$，飞龙号位于 $(a,b)$，一步内会有 7 种移动：

• $(p,q)$（2种方案）。

• $(p-1,q),(p,q+1),(p-1,q+1)$,

• $(p,q-1),(p+1,q),(p+1,q-1)$

注意此时合法区域变为了 $x\ge 0,y\ge 0$ 。

我们考虑对这个坐标再做一步转化。

我们发现我们现在的游走可以被拆分成 3 个分量，大概用生成函数写出来就是 $(1+x^{-1})(1+y^{-1})(x+y)$，然后中途的时候 $x$ 上的指数和 $y$ 上的指数始终要 $\ge 0$。我们发现 $(1+x^{-1}),(1+y^{-1})$ 只和其中的一个变量有关。

这诱导我们尝试把 $x+y$ 每一轮选什么枚举出来。

我们从 $(0,0)$ 开始画一条折线，每选一个 $x$ 就 $(+1,+1)$，每选一个 $y$ 就 $(+1,-1)$。我们这个时候再考虑 $(1+x^{-1})$ 和 $(1+y^{-1})$ 的约束是什么情况，他们会变成动态约束。但是你发现，大致就是折线向上走，$x$ 的约束变松，$y$ 的约束变严，折线向下走则反过来。我们把 $1+x^{-1}$ 的折线（选 $1$ $(+1,-1)$，选 $x^{-1}$ $(+1,+1)$）画出来，我们发现他应当满足在 $x+y$ 折线的下方，而 $1+y^{-1}$（选 $1$ $(+1,+1)$，选 $y^{-1}$ $(+1,-1)$） 折线应当在 $x+y$ 的上方。这实质上是一个不相交路径的约束！

我们发现最终 $x$ 和 $y$ 上的指数只和最后三个点相邻两者之间的距离有关。我们 $O(h)$ 枚举 $x+y$ 折线最终落在了哪里，然后 $LGV$ 引理计算不相交路径数即可。复杂度 $O(h)$。

题解二

solution by maspy

话不多说，我们直接上图。

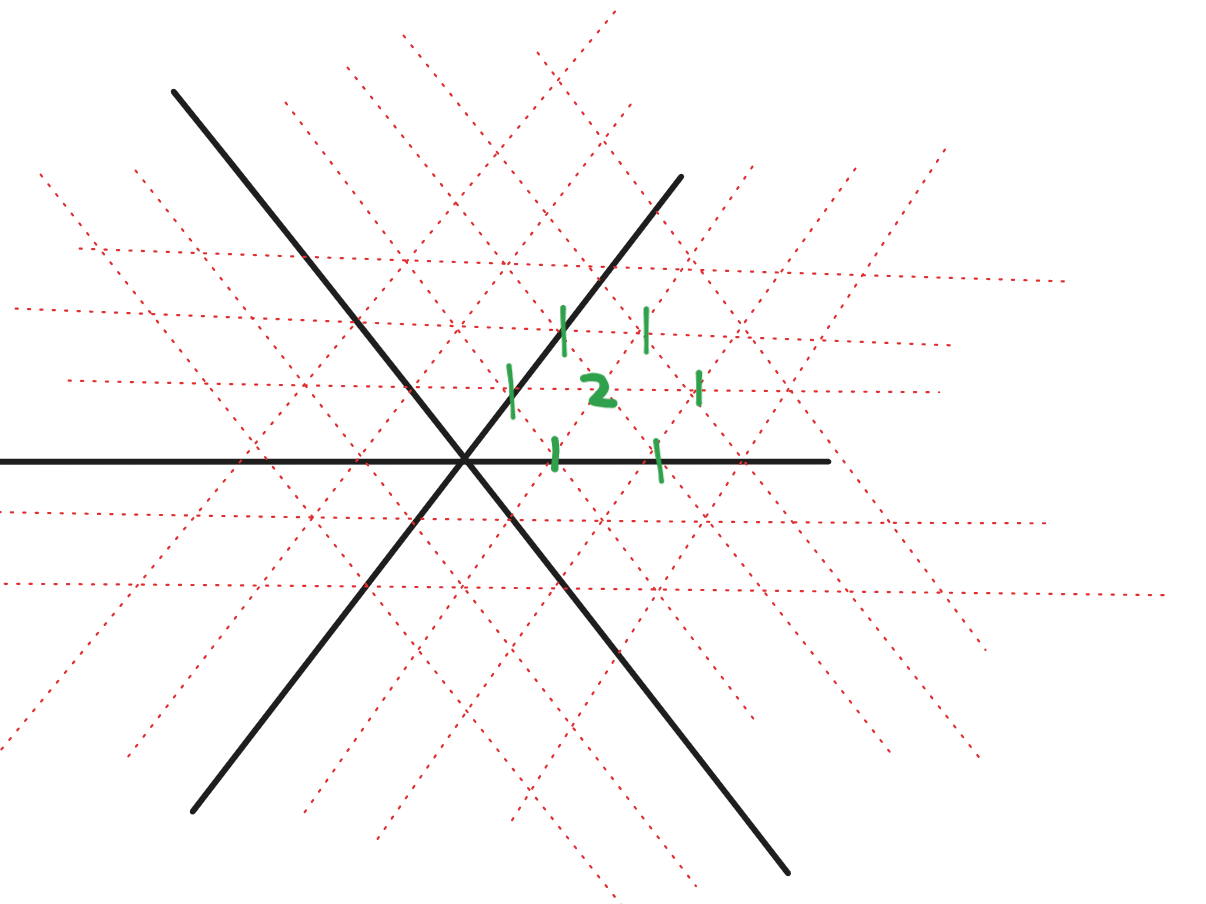
我们把原问题上的若干种转移拉伸缩放一下，画到三角格点的图上，就长这样。注意到这个转移是在任何方向上对称的！

我们如果把这个平面当成我们的 dp 数组的话，我们额外设置 5 个初值点，变成下图：

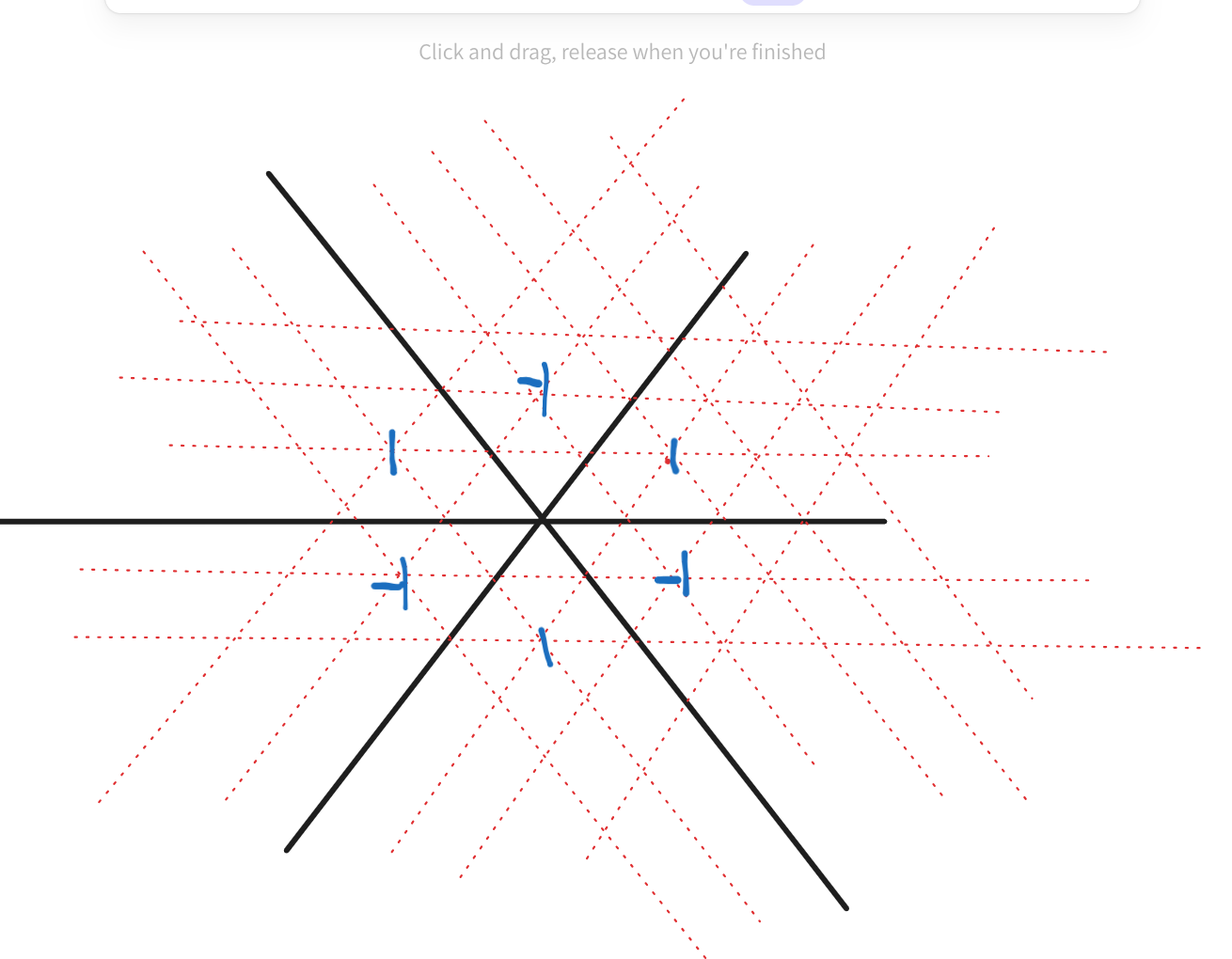
注意到在 dp 的转移过程中，正数和负数永远会在黑色的边界上抵消，这个黑色的边界会天然形成一个“不可穿越的结界”。但是它并非真的不可穿越，也就是说，我们不需要那个烦人的 $y\ge |x|$ 的约束了！

我们现在只需要用组合数计算一个点在 $h$ 步到另一个点的方案数即可。我们发现这个移动系数实际上可以分解为 $3$ 个分量的独立组合：

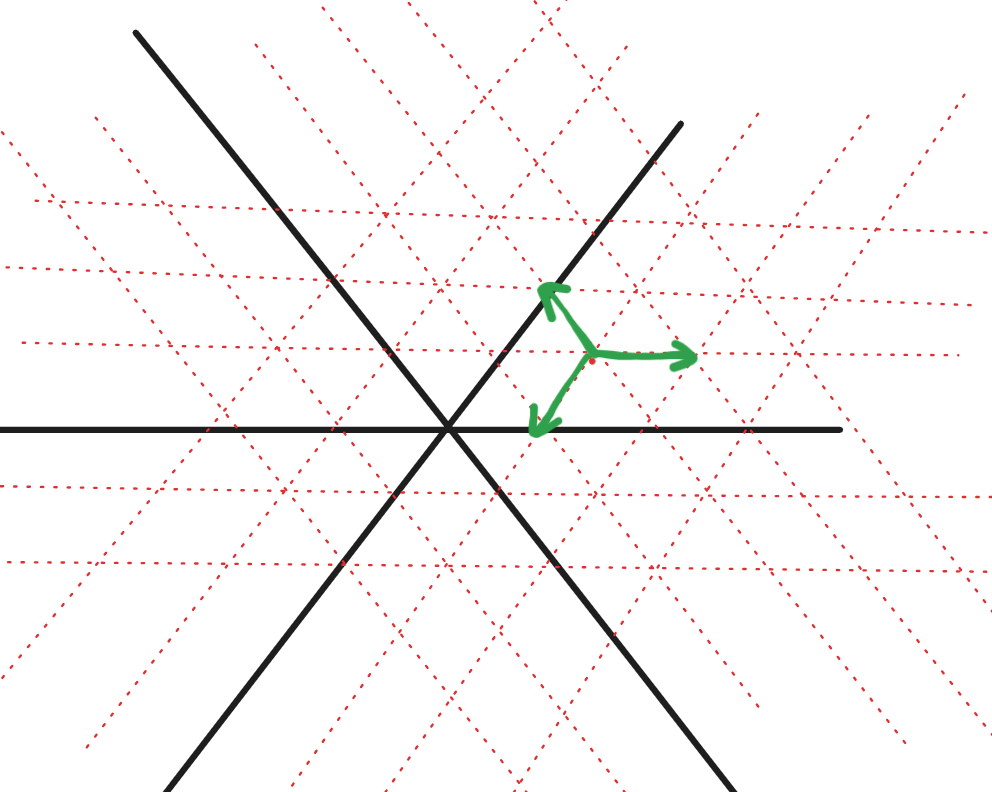
终点的坐标已经给我们带来两个方程，我们只需要枚举其中任意一个分量出现的数量，就可以计算剩下两个分量的出现次数，组合数计算即可。时间复杂度线性。