赛场设计

idea, solution, std, data by pp_orange

我们称“ $a$ 不能到达 $b$，$b$ 不能到达 $c$，$c$ 不能到达 $a$”为反三元环。

由于图是一个 DAG，所以对于任意一对节点 $(u,v)$ 必然有 $u$ 不能到 $v$ 和 $v$ 不能到 $u$ 中的至少一个。如果我们建立一张新图，把所有不可达关系全部画到这个图上，我们会发现这个图比竞赛图还密集。一些竞赛图的结论在这个图上仍然成立：

1、我们把这个图缩点之后会形成一个链。

2、这个图大小 $\ge 3$ 的 SCC 一定存在三元环。也就是原题中的反三元环

所以缩点后一定会形成一个每个 SCC 大小都小于等于 $2$ 的链结构。

考虑设计 $dp[i][j]$ 表示一共放了 $i$ 个点，链最后一层有 $j$ 个点的方案数，其中 $1\le j\le 2$，我们考虑先把 $i!$ 除掉，最后再乘回去即可，转移如下：

$$ dp[i+1][1] \gets dp[i][1]\times2^{i-1} + dp[i][2]\times2^{i-2} $$

$$ dp[i+2][2] \gets dp[i][1]\times2^{2(i-1)} + dp[i][2]\times2^{2(i-2)} $$

事实上我们还可以更进一步，把 $2^{\frac{i(i-1)}{2}}$ 也除掉，这样转移就是常系数的线性齐次转移了，可以用矩阵乘法优化。当然，在这个题没有必要，我们的瓶颈在于求阶乘。

这个题还有一些从最长反链 $\le 2$，于是最小链覆盖小于等于 $\le 2$ 的角度来刻画这个结构的，这里不多赘述。部分分设计主要为了一些指数级、高次多项式复杂度和固定模数算法。

最后复杂度为 $O(n)$ 或 $O(\sqrt n \log n)$（快速阶乘算法）。

交通管制

idea, solution, std, data by chenxinyang2006

考虑这样一个问题：假设给原图所有子集 $S \subseteq U$ 均赋了权重 $a_S$，并定义一张连通子图的权值是其所有边双对应的 $a$ 之积，并且我们还已经对所有 $S$ 知道了 $S$ 的边双连通边子图数量是 $b_S$，如何求原图所有边子图的权值和。

如果已经确定的边双给出的对 $U$ 的集合划分，把每个边双缩为一个点后，这一方案的 $a$ 之积是确定的，各个边双内部的连边方案数是对应的 $b$ 也是确定的，而边双之间的连边方案数相当于做生成树计数。不过如果这样看待问题并不好优化。

我们分阶段考虑这个问题，设 $p_0 \sim p_n$ 是 $n$ 个集合幂级数，$(p_i)_S$ 表示 $S$ 的导出子图的所有满足 只存在两端编号最大值不超过 $i$ 的割边 的边子图的权值和。最后希望计算 $p_n$，而 $p_0$ 因为不允许出现割边， $(p_0)_S=a_Sb_S$。

考虑 $p_{u-1} \to p_u$ 的变化：现在允许点 $u$ 的邻边有割边（但边的另一侧编号仍需 $ < u$）。如果将所有两端编号最大值为 $u$ 的割边断开，这张边子图将会分裂成若干连通块，根据连通块给出的点集划分设 $S = P \cap T_1 \cap T_2 \cap ... \cap T_k$，其中 $u \in P$，所有 $P,T_i$ 两两无交。那么这张边子图在所有 $P$ 或 $T_i$ 的部分都符合 $p_{u-1}$ 的限制，这是递归到子问题的形式，并且这个划分当然是唯一的。

于是要计算 $(p_u)_S$ 只需枚举 $S$ 像这样的集合划分，对应的所有边子图权值和是 $(p_{u-1})_P \prod\limits_{i=1}^k (p_{u-1})_{T_i} cof(u,T_i)$，其中 $cof(u,T_i)$ 表示选一个 $v \in T_i,v < u$ 新连上 $(u,v)$ 这条子图中的割边的方案数，其实也就是原图中 $u$ 与多少在 $T_i$ 内且编号小于自己的点有连边。

那么设 $(q_{u-1})_S=[u \notin S] (p_{u-1})_S \cdot cof(u,S)$，在只考虑 $u \in S$ 的项的意义下，$p_u=p_{u-1} \times (\exp q_{u-1})$。注意若 $u \notin S$ 那么上述分析其实都无效，但当然 $(p_u)_S=(p_{u-1})_S$。

于是计算 $n$ 次集合幂级数 exp 以及子集卷积即可解决上述问题。

称该由 $p_0$ 计算 $p_n$ 的操作为 “边双连通-连通变换”。

接下来考虑 数边双连通子图，注意在上述问题中若取所有 $a_S=1$，计算出的 $(p_n)_S$ 应为 $S$ 导出子图的连通边子图数，这可以 $\Theta(2^nn^2)$ 计算。注意上述过程是可逆的，知道 $p_i$ 同样只需进行一次集合幂级数 exp 和一次子集卷积即可求出 $p_{i-1}$。于是逐步倒推，在已知 $p_n$ 的前提下进行 $n$ 次集合幂级数 exp 以及子集卷积可以倒推得到 $p_0$，称为反向的 “边双连通-连通变换”。

对于本题，限制相当于是一些点对必须连通，以及一些点对的边简单路径必须不唯一。方便起见我们先假定要求选出的边子图连通。

注意到若一个点对已经连通，其间的边简单路径唯一充要于将每个边双缩为点之后，在得到的边双树上两个点简单路径上经过的边双大小均为 $1$。那么对于确定的边双树，称大小 $>1$ 的边双为黑点，大小 $=1$ 的边双为白点，$u,v$ 间只存在一条边简单路径当且仅当它们所属同一个极大白色连通块。

一张边子图根据极大白色连通块和黑色点给出了对原图点集 $U$ 的划分 $U=P_1 \cup P_2 \cup ... \cup P_m \cup Q_1 \cup Q_2 \cup ... \cup Q_k$。$P_i$ 对应极大白色连通块，$Q_i$ 对应一个大小大于 $1$ 的边双。

那么 $c_i=2$ 的限制相当于说不能出现某个 $P_i$ 满足存在限制 $(s_j,t_j,2)$ 且 $s_j,t_j \in P_i$。假设一张边子图给出的对 $U$ 的划分确定，可以据此判断其是否合法。

假设划分确定，某个 $P_i$ 内部的连边数相当于这个点集导出子图的生成树计数，直接使用矩阵树定理计算是 $\Theta(2^nn^3)$ 的，其实也可以 $\Theta(2^nn^2)$ 不过不重要。某个 $Q_i$ 内部的连边数即数边双连通子图，可以 $\Theta(2^nn^3)$ 全部计算出。

之间的连边还是把一个 $P_i,Q_i$ 缩成一个点之后相当于做生成树计数。但注意因为要求 $P_i$ 是极大的，不能将两个极大白色连通块相连！

回忆经典题 “$n$ 种颜色的小球第 $i$ 种有 $a_i$ 个，有多少种排列小球的方式使得没有同色小球相邻” 是如何解决的：容斥枚举一些小球对同色且相邻。这两个问题非常类似，因此处理这一限制也可以考虑容斥。

把连边看作两个阶段：第一阶段只能在 $P_i$ 间连边，连边边权为 $-1$，第二阶段可以任意连边，连边边权为 $1$。

那么对于连出来边集一致（忽略边权）的一些生成树，假设其将两个极大白色连通块相连，这条边既可以在第一阶段连也可以在第二阶段连，因此权重抵消了。

于是设 $f'_S$ 表示 $S$ 导出子图生成树计数，$f_S=f'_Svalid(S)$，$valid(S)$ 表示 $S$ 是否能作为一个极大白色连通块，$g_S$ 表示 $S$ 导出子图的边双连通边子图数量。设 $transfer(F,c)$ 为将 $F$ 进行每额外选一条割边贡献乘上 $c$ 的正向 “边双连通-连通 变换” 后得到的集合幂级数。原问题的答案是 $transfer(transfer(f,-1)+g,1)_U$。

原问题未必要求选出的边子图连通，注意到 $transfer(transfer(f,-1)+g,1)$ 相当于对所有 $S \subseteq U$ 计算了 $S$ 导出子图中有多少连通边子图满足所有 $(s_j,t_j,2)$ 的限制，只要 $s_j,t_j \in S$。原图任意的边子图根据连通块给出了对 $U$ 的点集划分，一些划分出来的点集可能不满足连通性限制，对所有满足连通性限制的点集的答案做 exp 即可。

时间复杂度 $\Theta(2^nn^3)$。更劣的 $\Theta(3^nn)$ 在此数据范围下无法区分，也可通过。

如果有疑惑，更详细的分析以及一些背景知识介绍见 apio2025 我的讲课。

百里马拉松

idea, solution, std, data by _LHF_

本题标算为 $O(\frac{n\log n}{\log \log n})$，然而出题人因为水平问题无法区分该做法和 $O(n\log n)$ 的做法，出题人在此谢罪。

建议先阅读论文《浅谈树上邻域问题的一种基于长链剖分的解法》。

考虑对树进行长链剖分，

首先对于一个询问 $(x,d)$，如果 $x$ 的高度 $\ge d$，那么 $(fa_x,d)$ 和 $(x,d)$ 结果相同，此时不妨令 $x\to fa_x$，不断这么做直到不能这么做位置，该过程可以用倍增做到 $O(\log n)$。

简单转化一下，相当于是每条长链都挂了一条额外链，然后只需要处理所有挂在这个长链上的询问。

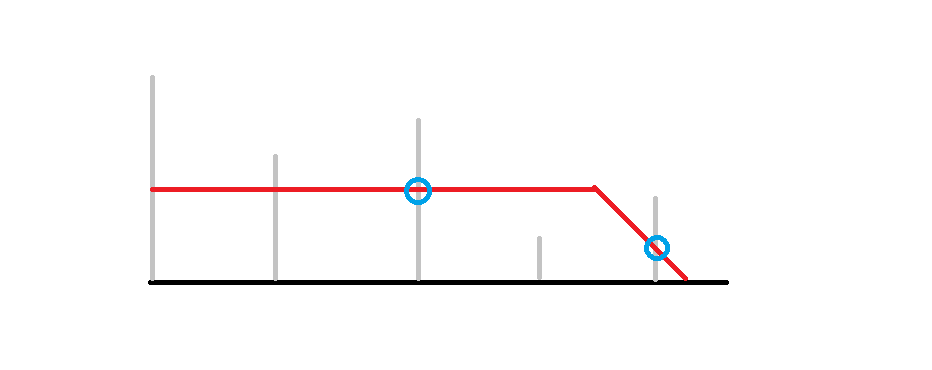
对于处理该长链子树外部贡献的方法，详见我的论文。

找到 $(x,d)$ 左侧和右侧第一个碰到的点，然后考虑将询问拆成三个部分，中间那部分直接二区间合并分治即可，这样可以做到三次合并解决。

然后可以类似我在营员交流中提到的技巧，改成一次合并，总复杂度仍然是 $n\log n$，不过常数过大，所以无法接受。

事实上我们可以将该问题转化为一个树上祖先后代链查询的问题，具体来说，对于一条额外链，我们把每个位置都看成一个点，然后类似论文中“强制在线处理方法”连边，转化成树上链查询问题，用树上二区间合并分治即可。

实际上还能做得更好，考虑倍增分块，对于长度为 $len$ 的额外链，找到最小的 $b$ 满足 $B^b\ge len$，然后将该额外链的长度扩充到 $B^b$。这样本质不同的额外链长度数量就不超过 $\log_Bn$ 条了，可以直接暴力枚举跳到了哪一个长度上，标算实现是 $O(n(2B+\log_B n+C))$，其中 $C$ 是一个和 $n,B$ 无关的常数。

然后我们简单处理一下即可，$B=2$ 时复杂度为 $O(n\log n)$。

注意到 $B$ 不一定要取到 $2$，当 $B$ 取到 $(\log n)^{eps}$ 时理论复杂度为 $O(\frac{n\log n}{\log\log n})$。然而该做法常数较大，所以出题人几乎无法区分该做法和 $O(n\log n)$ 的做法。

如果有人有更优的做法，欢迎和出题人联系。