曾经有人反映说看不懂这题题解,我来写一个(
一些基础观察
首先可以只保留强连通分量里的边,考察每个强连通分量,可能有几种情况:
- 是一个“循环”,存在一个 $k$ 使得距离 $\bmod k$ 相同的点字符相同。此时生成的字符串数量是有限的 $k$ 个。
- 包含至少两个“循环” $A$ 和 $B$,可以生成 $A^{\infty},(AB)^{\infty},(AAB)^{\infty},(AAAB)^{\infty},\cdots$,此时有一个在集合中的下界 $A^{\infty}$。
- 可以生成 $(ABC)^{\infty},(ABBC)^{\infty},(ABBBC)^{\infty},\cdots$,此时有一个不在集合里的下界 $(AB^{\infty}C)^{\infty}$。
假设我们已经特判掉了第 1 种情况,考虑 2 和 3,我们可以求出一个最终集合的“上界”,再把情况 1 的串判断能否小于上界。
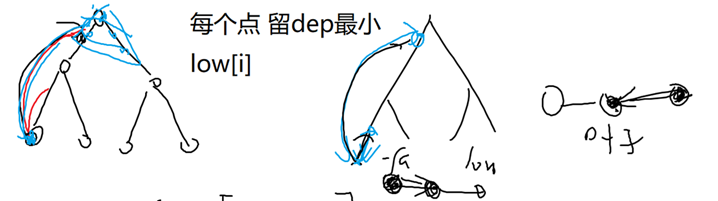
为了求出 2 和 3 的最小字符串,想做的是求出每个点开始,走一个字典序最小的无限环 是什么样的路径。
设 $f(u,i)$ 表示 $u$ 开始,走 $i$ 步得到的字符串,最小是什么。这里只记所有 $f(u,i)$ 之间的大小关系。
转移每步从 $i\to i+1$ 可以递推,并且只要做 $O(n)$ 轮,直到 $f(u,i)$ 不再变化。
然后建一张新的有向图,图上的每个点表示一个 $f(u,i)$ 的值,每个点仅有一条出边,指向它在原图中最小的出边的 $f$ 值。
考虑一个强连通分量中的最小字符串:
- 如果走的是一个 $\rho$ 形,对应情况 3。
- 如果走的是一个 $o$ 形,且一个强连通分量中有 $\ge 2$ 个不同的环,对应情况 2。
- 否则,对应情况 1。
这样可以得到 $O(nm)$ 做法。
这里看似需要一些后缀数据结构来比较,但实际上,我们可以把所有点一起做这个过程,这样就同时维护了所有点 $f$ 的值的大小关系。
优化
下面考虑优化求出 $f$ 的过程。
我们不再考虑一轮一轮递推出 $f$,而是维护当前所有点 $f$ 的相对大小关系。此时所有点会根据 $f$ 分为若干等价类,同时维护每个等价类的最小出边。
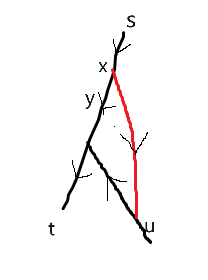
考虑一个“等价类分裂”操作:假设一开始某个集合 $S$ 中所有点的 $f$ 是相等的,现在把集合 $S$ 分成两个集合 $S_0,S_1$,其中 $f(u) < f(v) (u\in S_0,v\in S_1)$。
这会造成 $S$ 中所有点的前驱的 $f$ 值可能发生变化。从而发生更多的“等价类分裂”的连锁反应。
初始把所有点当成一个等价类,然后每次把最小的字母分裂出去,并且处理所有“等价类分裂”的连锁反应。
如果每次暴力处理分裂,直到不再分裂,能求出所有点的 $f$。时间复杂度仍为 $O(nm)$。
但是这里可以“启发式分裂”:选择 $S_0,S_1$ 中 size 更小的那一边,遍历 $S_i$ 的所有前驱,只考虑这些前驱的等价类的变化。
具体过程如下:
- 维护一个队列,存储所有分裂操作 $S\to S_0,S_1$。
- 一开始插入所有“分裂一个最小字母”的操作,这部分大小 $\le n$ 个。
- 若 $|S_0| \le |S_1|$:
- 遍历所有 $u\in S_0$ 的入边。
- 假设有 $x\to u,x\in T$,且 $T\to S$,则 $T$ 的出边可能会修改。
- 由于 $S_0$ 更小,对于所有 $x$,等价类都会修改为 $T_0$,其中 $T_0 < T$。
- 若 $|S_0| > |S_1|$:
- 若对于 $x$,所有 $x$ 向 $S$ 的出边都指向 $S_1$,则等价类会修改为 $T_1$,其中 $T_1 > T$。
- 遍历所有被影响的等价类 $T$,可能被分裂成两个集合 $\{T_0,T\}$ 或 $\{T,T_1\}$。若两个集合都不为空,则需要分裂。
- 取出两个集合中更小的那一个,建立一个新的等价类。
- 以分成 $\{T_0,T\}$ 为例:
- $|T_0| \le |T|$:建立一个 $T_0$ 的等价类。
- $|T_0| > |T|$:遍历整个 $T$,求出 $T\setminus T_0$,建立 $T\setminus T_0$ 的等价类。此时原来的 $T$ 大小减半。
- 然后在队列中 push 一个分裂操作。
时间复杂度 $O(m\log n)$。

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号